Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.
직사각형 최대 넓이 찾기
Example 1:
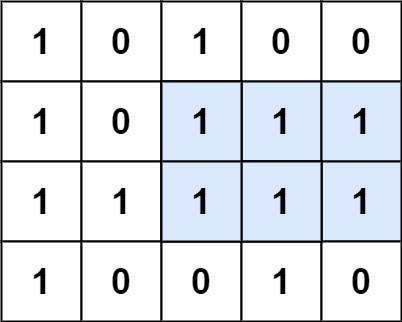
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] Output: 6
Explanation: The maximal rectangle is shown in the above picture.
Example 2:
Input: matrix = [] Output: 0
Example 3:
Input: matrix = [["0"]] Output: 0
Example 4:
Input: matrix = [["1"]] Output: 1
Example 5:
Input: matrix = [["0","0"]] Output: 0
Constraints:
- rows == matrix.length
- cols == matrix.length
- 0 <= row, cols <= 200
- matrix[i][j] is '0' or '1'.
문제 풀이
- 난이도 hard
- 역시나 어려웠다. dp를 사용하는 문제지만 정사각형 넓이 구하기와는 접근 방식이 다르다.
- 사용한 알고리즘은 히스토그램을 이용한 직사각형 최대 넓이 구하기
www.geeksforgeeks.org/largest-rectangle-under-histogram/?ref=lbp
Largest Rectangular Area in a Histogram | Set 2 - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
set1은 divide and conquer방식이고 set2는 stack을 이용한 방식이다. 여기선 set2방법인 stack을 사용했다.
- 히스토그램 사용방법만 안다면 접근은 간단하다.
1. row별로 히스토그램을 만든다.
2. 히스토그램 최대 넓이 구하기에 row를 넣어서 최대 넓이를 구한다.
2의 구현방법부터 알아보자.

히스토그램이 좌측과 같다면 여기서 최대 직사각형 넓이는 4*3 = 12이다.(모든 직사각형의 width는 1로 가정한다.)
스택을 이용해서 접근해보자.
직사각형 최대 넓이는 특정 구간에서 최소 높이에 따라 결정됨을 알 수 있다. 좌측 그림에서 보자면 6 - 2 - 5 - 4 - 5가 있다면 2가 넓이를 좌우한다.
bar의 높이가 > 가 되면 현재 인덱스보다 left에 있는 막대기가 최소 길이라고 가정하여 넓이를 구해야 한다. 왜냐! 더 작은 높이가 등장했다는 뜻이기 때문. 최대 넓이 구해야 하니까 직사각형 넓이가 나오는 모든 경우의 수를 따져줘야 한다.
따라서 넓이를 측정하는 시점은 그림에선 6>2, 5>4, 5>1일 것이다.
정리:
1) 만약 스택이 비어있거나 스택의 top보다 < cur 길이라면 스택에 현재 인덱스를 push
2) 스택의 top보다 > cur 길이라면 넓이를 한 차례 구해준다. 언제까지? cur 길이보다 작은 스택값이 나올 때 까지
2-1) 스택의 top을 저장한 후 pop
2-2) 현재 인덱스보다 left에 있는 친구들로 만들 수 있는 최대 넓이 = 스택 탑 * 가로 길이
2-3) max 업데이트
3) 스택에 남은 거 처리하기
3-1) 2와 동일
int getMaxArea(int hist[], int n)
{
stack<int> s;
int max_area = 0; // Initialize max area
int tp; // To store top of stack
int area_with_top; // To store area with top bar
// as the smallest bar
int i = 0;
while (i < n)
{
// 현재 bar가 stack top의 bar보다 크거나
// 스택이 비어있다면, push
if (s.empty() || hist[s.top()] <= hist[i])
s.push(i++);
// 현재 bar가 stack top bar보다 작다면
// 스택의 top에 위치한 bar가 최소 높이 일때 직시각형 넓이를 구한다.
// 현재 'i'가 right idx, 스택 top의 인덱스가 left idx이다.
else
{
tp = s.top(); // store the top index
s.pop(); // pop the top
// 스택 탑에 있는 높이가 최소 높이라고 가정했을 때 직사각형 넓이 구하기
area_with_top = hist[tp] * (s.empty() ? i :
i - s.top() - 1);
// max 넓이 업데이트
if (max_area < area_with_top)
max_area = area_with_top;
}
}
// 스택에 남아 있는 bar 높이를 pop해서
// pop된 bar가 최소 높이라고 가정하여 넓이를 구한다.
while (s.empty() == false)
{
tp = s.top();
s.pop();
area_with_top = hist[tp] * (s.empty() ? i :
i - s.top() - 1);
if (max_area < area_with_top)
max_area = area_with_top;
}
return max_area;
}
이제 row별 히스토그램을 구해보자 아래 그림이 input이라면

0 1 1 0
1 2 2 1
2 3 3 2
3 4 0 0 =>이런 식으로 히스토그램을 만들 수 있다.
전체 코드:
class Solution {
public:
int useHistogram(int row[], int n){
int maxArea=0, tmpArea=0;
stack<int> s;
int i=0;
while(i<n){
if(s.empty() || row[i] > row[s.top()]){
s.push(i++);
}else {
int leftIdx = s.top();
s.pop();
tmpArea = row[leftIdx] * (s.empty()? i : i - s.top() - 1);
maxArea = max(maxArea, tmpArea);
}
}
while(!s.empty()){
int leftIdx = s.top();
s.pop();
tmpArea = row[leftIdx] * (s.empty()? i : i - s.top() - 1);
maxArea = max(maxArea, tmpArea);
}
return maxArea;
}
int maximalRectangle(vector<vector<char>>& matrix) {
int rows = matrix.size();
if(rows == 0){
return 0;
}
int cols = matrix[0].size();
int dp[rows][cols];
memset(dp, 0, sizeof(dp));
int result = 0;
//make histogram
for(int i=0; i<rows; i++){
for(int j=0; j<cols; j++){
if(i==0){
dp[0][j] = matrix[0][j] -'0';
}else {
if(matrix[i][j] == '1'){
dp[i][j] = (matrix[i][j] - '0') + dp[i-1][j];
}
}
}
//get max area using histogram
result = max(result, useHistogram(dp[i], cols));
}
return result;
}
};'알고리즘 문제풀이 > leetcode' 카테고리의 다른 글
| [leetcode 75] Sort Colors (0) | 2020.10.28 |
|---|---|
| [leetcode 72] Edit Distance (0) | 2020.10.28 |
| [leetcode 53] Maximum Subarray (0) | 2020.10.27 |
| [leetcode 62]Unique Paths (0) | 2020.10.27 |
| [leetcode 64] Minimum Path Sum (0) | 2020.10.27 |

댓글