방향이 있는 그래프에서 싸이클을 찾는 방법을 알아보자.
Using BFS
Kahn 알고리즘을 사용한다.
www.geeksforgeeks.org/detect-cycle-in-a-directed-graph-using-bfs/
Detect Cycle in a Directed Graph using BFS - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
indegree와 outdegree
indegree: vertex를 기준으로 들어오는 방향의 화살표
outdegree: vertex를 기준으로 나가는 방향의 화살표
Khan 알고리즘
indegree와 위상정렬 + BFS를 사용한다.
DAG(directed acyclic graph)는 indegree가 0인 vertex와 out degree가 0인 vertex가 적어도 한개는 존재한다.
증명:
outdegree가 0인 vertex -> 도착점
indegree가 0인 vertext -> 시작점
두 노드 사이에서 cycle이 발생할 순 있지만 어째됐든 최소 도착점, 시작점이 하나씩은 있어야 DAG를 만족할 수 있다.
알고리즘은 위상정렬을 찾아서 진행한다.
1. 모든 vertex에 대해 incoming edges(in-degree)를 센다. visited node의 cnt를 0으로 초기화.
2. in-degree가 0인 것이 시작 노드. 0인 경우 queue에 푸쉬한다.
3. q가 NOT EMPTY인 경우
3-1. front = q. front()를 저장. visited node cnt를 1만큼 증가시킨다. pop
3-2. front의 인접 노드에 대해 indegree값을 1만큼 감소시킨다.
3-3. 만약 감소시킨 indegree가 0이라면 queue에 푸쉬한다.
4. visited node cnt가 전체 노드의 수와 다르면 cycle이 존재한다는 의미이다.
혹은 indegree 배열 중에 0보다 큰 수가 있다면 cycle이 존재한다는 의미이다.
(순서대로 indegree를 전부 지웠기 때문)
Using DFS
# 1
www.geeksforgeeks.org/detect-cycle-in-a-graph/
Detect Cycle in a Directed Graph - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
핵심: backedge가 있는지 확인한다. 백엣지란 자식노드에서 조상노드로 향하는 엣지를 의미한다.
구현을 위해 필요한 것은 2종류의 배열: 방문여부를 체크하는 visited 배열과 사이클 여부를 확인하는 recStack배열
하나의 노드에 들어가서 visit체크를 하고 dfs를 시작한다. dfs를 진행하면서 만나는 모든 노드를 recStack에 체크하는데 만약 이미 visit된 노드가 다시 등장한다면 cycle이 존재함을 의미한다.
알고리즘: cycle이 존재한다면 true, 그렇지 않다면 false
1. isCyclic 함수:
1-1.visited와 recStack을 전부 false로 초기화.
1-2. 모든 노드에 대해 싸이클이 존재하는 여부를 dfs로 확인한다.
2. dfs: cycle이 존재한다면 true, 그렇지 않으면 false
2-1. 현재 노드를 visited체크하고 recursion 스택에도 표기.
2-2. 현재노드와 인접한 노드 중 방문하지 않은 노드에 대하여 recursive하게 dfs를 호출
2-3. 인접노드가 이미 recStack에 있다면 true를 리턴(사이클 존재)
# 2
https://leetcode.com/problems/all-paths-from-source-lead-to-destination/description/
All Paths from Source Lead to Destination - LeetCode
Can you solve this real interview question? All Paths from Source Lead to Destination - Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
이 문제를 풀다가 발견했다.
https://en.wikipedia.org/wiki/Introduction_to_Algorithms
요 책에 나온 방법이다. 알고리즘계의 수학의 정석!
vertex의 색상을 3가지로 구분한다.
white: vertex which is not processed. 아직 탐색이 진행되지 않은 상태로 vertex의 디폴트 상태이다.
gray: vertex which is being processed. 자식 vertex의 탐색이 진행중인 상태로 아직 recusrion stack에 있다.
black: vertex which had been processed. 자식 노드까지 탐색이 종료된 상태이다.
case 1) cycle이 존재
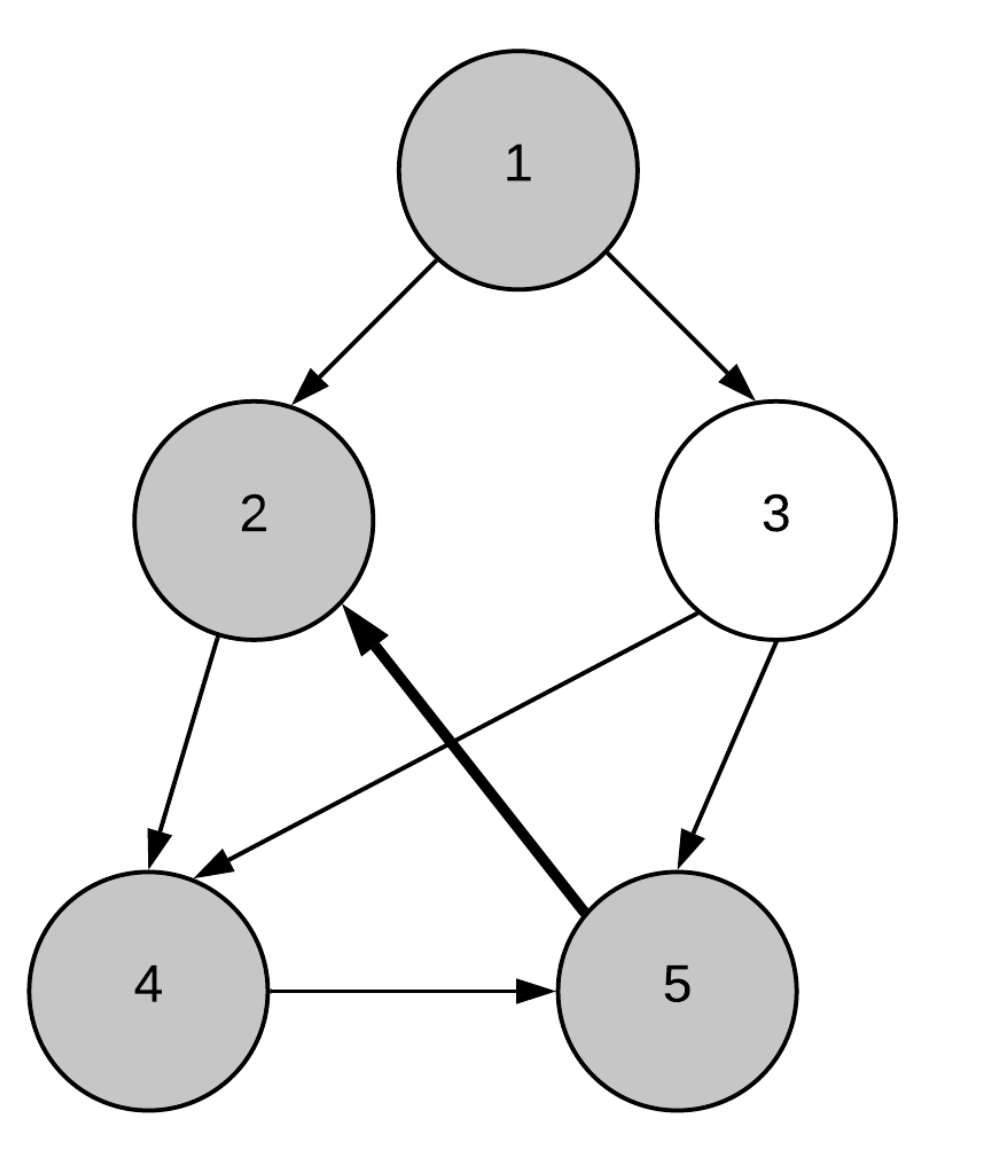
1부터 탐색을 시작한다면 1->2->4->5로 탐색할 것이다.
5는 다시 2를 탐색하는데 2는 지나온 경로에 존재하는(recursion stack에 존재) 노드이다. 따라서 cycle이 존재함을 알 수 있다.
case 2) cycle 없음
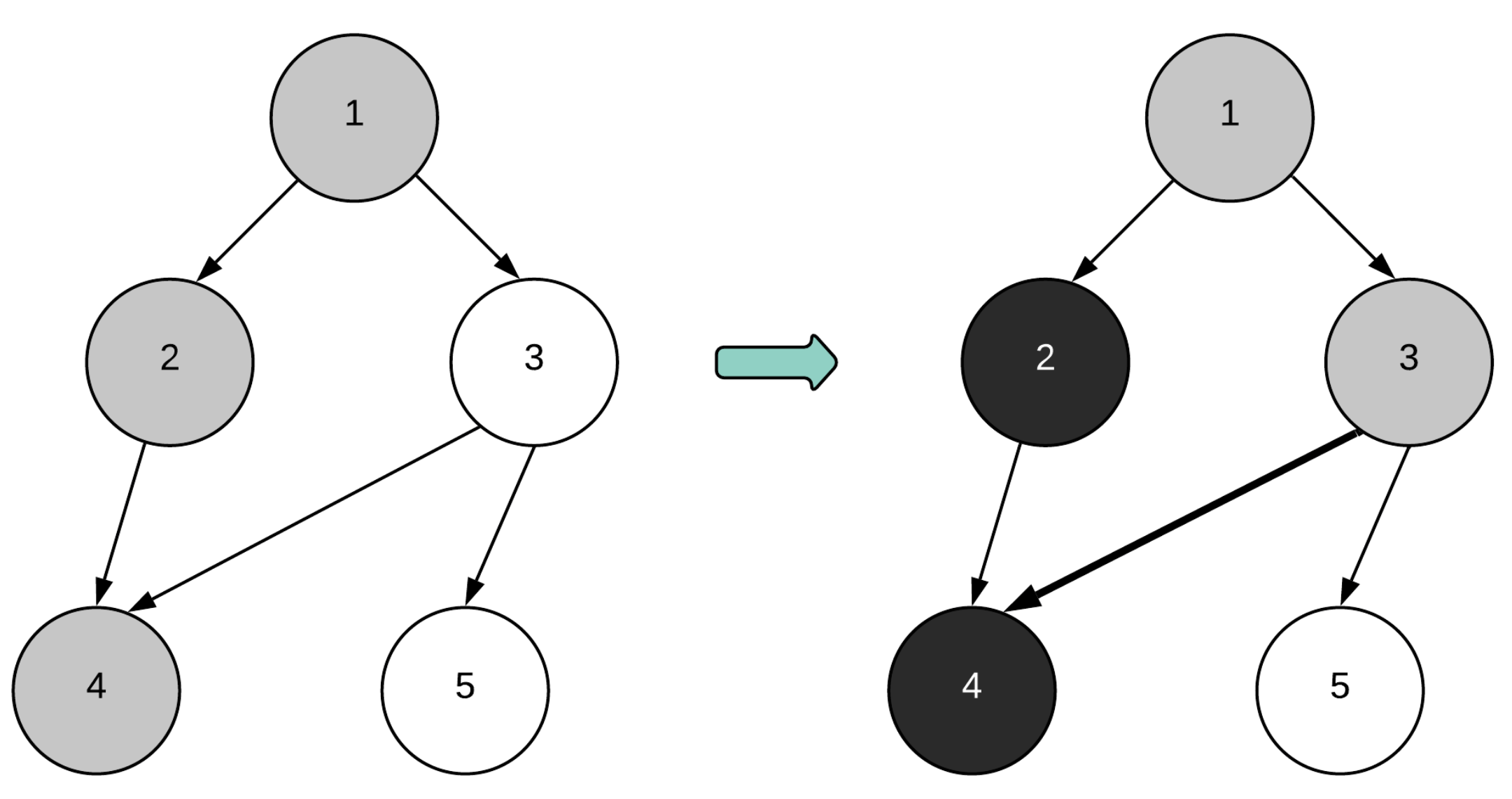
1부터 탐색을 한다면 왼쪽 그림에서는 1->2->4로 탐색할 것이다. 4에서 탐색이 종료되고 1까지 backtracking을 하면서 state를 black으로 변경한다.
이제 오른쪽 그림과 같이 1->3->4로 탐색하게 될 텐데 3은 이미 탐색이 종료된 4로 향하므로 cycle이 존재하지 않는다.
sudo-code
boolean isAcyclic(int cur, List<Integer>[] adj, Color[] states){
if(states[cur] != white){
return states[cur] == black;
// 탐색이 종료된 node를 탐색한다면 cycle이 존재하지 않음
}
states[cur] = gray; // process start
for(int next: adj[cur]){
if(!dfs(next, adj, states)) return false;
// 중간에 cycle이 존재한다면 return false;
}
states[cur] = black; // process end
return true;
}수도 코드를 작성한다면 위와 같을 것이다.
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최단 경로 역추적 (0) | 2021.04.11 |
|---|---|
| [알고리즘] 이분탐색 Binary Search (0) | 2021.02.01 |
| [알고리즘] 선형 자료 구조에서 탐색(Search) (0) | 2021.01.21 |
| [알고리즘] Dijkstra 다익스트라 알고리즘 (0) | 2020.12.30 |
| [알고리즘] 정렬 - quick sort (0) | 2020.11.29 |
댓글