- 한 정점에서 여러 개의 다른 정점까지의 최단 거리를 구하는 알고리즘 (single source shortest path)
- 간선에 양의 가중치가 존재한다. (음의 가중치 간선이 존재해서는 안된다.)
- 구현시 배열 혹은 힙(우선순위큐)을 사용한다.
초기화
dis[V]: 시작점으로부터 V까지의 거리를 저장하는 배열
- V가 시작점인 경우만 0, 나머진 INF초 초기화
chk[V]: V를 선택해서 계산을 했었는지에 대한 배열
로직
1. chk가 false인 정점 중 dist가 가장 작은 정점 x를 선택한다.
2. x와 인접한 정점의 dist를 갱신한다.
for( a : adj[x])
dis[a.v] = min(dis[a.v], dis[x.v] + a.cost)
3. chk를 true로 바꾼다.
4. 모든 chk가 true가 될 때 까지 반복한다.
연결 경로 저장하기
인접행렬로 (연결된 노드,비용)을 저장해도 되고
배열에 비용을 저장해도 된다. 이 방법의 경우 노드 사이에 경로가 여러 개 존재할 수 있으므로 최소 비용을 저장해야 한다.
인접행렬
vector<pair<int, int>> adj[MAX];
adj[i].push_back({j,c})
배열
arr[i][j] = c
예시
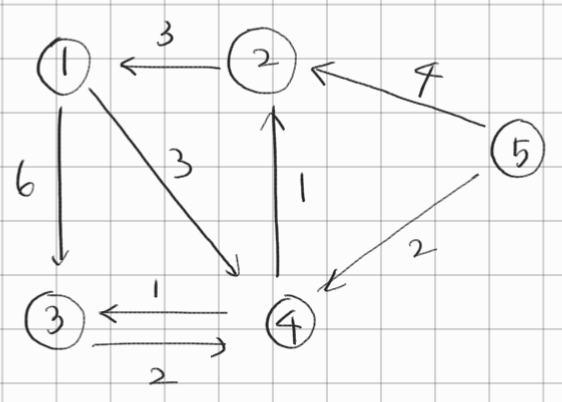
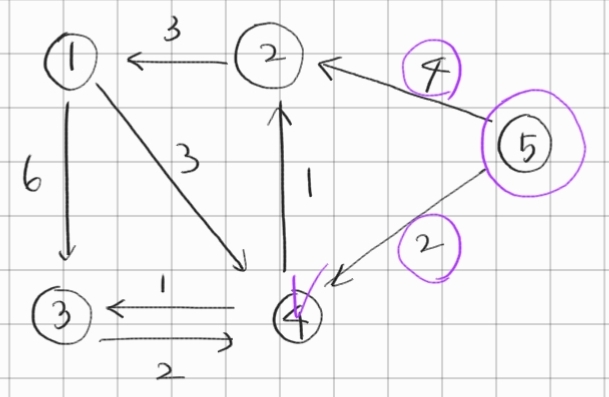
| 5 | 4 | 3 | 2 | 1 |
| 0 | 2 | INF | 4 | INF |
1. 시작점은 0으로 초기화하고 연결된 정점들 가중치만 표시한다. 나머진 무한대로 초기화
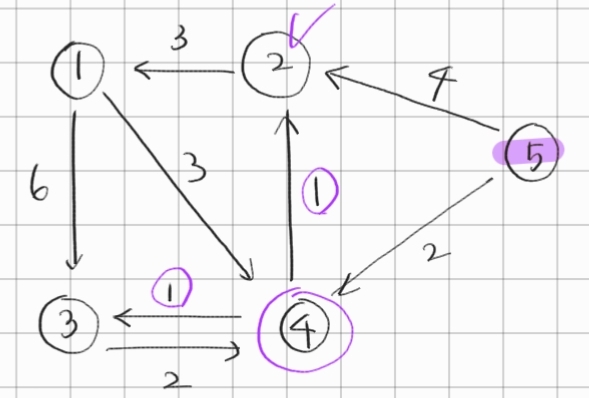
| 5 | 4 | 3 | 2 | 1 |
| 0 | 2 | 3 | 3 | INF |
2. 가중치가 가장 작은 4번을 택한다. 4번에 연결된 3과 2를 업데이트한다.
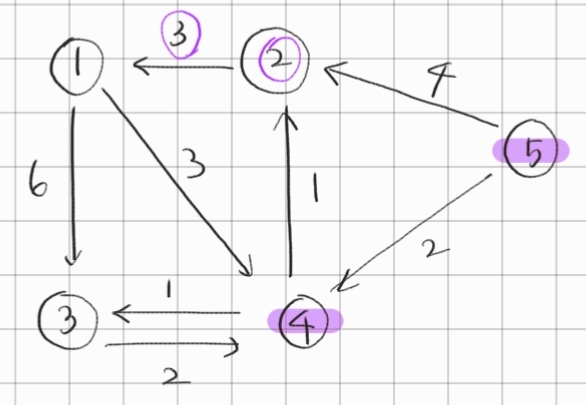
| 5 | 4 | 3 | 2 | 1 |
| 0 | 2 | 3 | 3 | INF |
3. (가중치가 같다면)2번과 3번 중 번호가 더 작은 2번을 택한다. 1번이 업데이트 된다.
정답:
| 5 | 4 | 3 | 2 | 1 |
| 0 | 2 | 3 | 4 | 6 |
구현
1. 배열 사용
- 시간복잡도 O(N^2)
const int INF = 1e9;
int start;
vector<pair<int, int>> v[100];
int dis[100];
bool visited[100];
void Dijkstra(int v)
{
dis[start] = 0;
for (int i=1; i<=v; i++)
{
int minCost = INF, minV = -1;
//방문하기 않은 노드 중 최소비용인 노드 찾기
for(int j=1; j<=v; j++){
if(chk[j]) continue;
if(dis[j] < minCost) minCost = dis[j], minV = j;
}
//최소 비용 노드의 인접 노드들 update
for(auto [next, cost] : adj[minV]){
dis[next] = min(dis[next], dist[minV] + cost);
}
chk[minV] = true;
}
}
int main(void)
{
int v,e;
scanf("%d%d", &v, &e);
for(int i=1; i<=v; i++) dis[i] = INF;
for(int i=1; i<=e; i++){
int a,b,c;
scanf("%d%d%d", &a,&b,&c);
adj[a].push_back({b,c});
}
Dijkstra(start);
return 0;
}
2. 힙 사용 - 우선순위큐를 사용한다.
- 시간복잡도 O(N*logN)
#include <stdio.h>
#include <queue>
#include <vector>
#define INF 1000000
using namespace std;
int dis[100];
bool chk[100];
vector<pair<int, int>> arr[100];
priority_queue<pair<int, int>> pq;
void Dijkstra(int start)
{
dis[start] = 0;
pq.push({0, start});
while (!pq.empty())
{
int cur = pq.top().second;
pq.pop();
if (chk[cur])
continue;
chk[cur] = true;
for (auto [next, cost]: arr[cur])
{
dis[next] = min(dis[next], dis[cur] + cost);
q.push({-dist[next], next});
}
}
}
int main(void)
{
int n, v_size;
scanf("%d%d", &n, &v_size);
for (int i = 1; i <= v_size; i++)
{
dis[i] = INF;
}
for (int i = 0; i < n; i++)
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
arr[u].push_back({v, w});
}
Dijkstra(0);
return 0;
}'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 이분탐색 Binary Search (0) | 2021.02.01 |
|---|---|
| [알고리즘] 선형 자료 구조에서 탐색(Search) (0) | 2021.01.21 |
| [알고리즘] 정렬 - quick sort (0) | 2020.11.29 |
| [알고리즘] 정렬 - Merge Sort (0) | 2020.11.01 |
| [알고리즘] 0-1 BFS (0) | 2020.10.29 |


댓글