서로소 집합 Disjoint Set
공통 원소가 없는 부분집합들로 이뤄진 자료구조
1) 구현
집합 구현시 배열, 연결 리스트 등 여러가지 형태가 있지만 트리를 이용하여 주로 구현한다.
ex) {1,2,5,6,8} {3,4} {7}의 표현
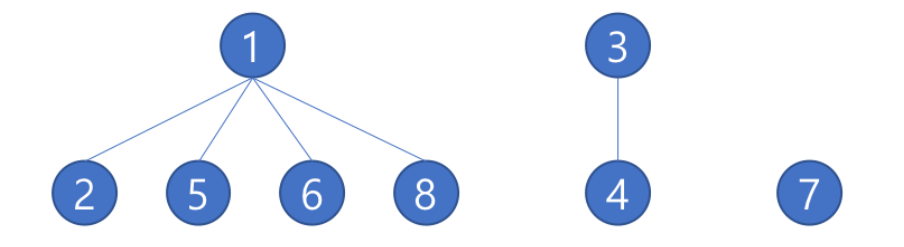
최상단 노드인 1과 3, 7이 각 부분집합의 id라고 생각하면 된다.
Union-Find
disjoint set을 표현할 때 사용되는 알고리즘
Union-Find 연산
1. find
어떤 원소가 주어졌을 때 이 원소가 속한 집합을 반환한다. 집합을 반환하기는 힘드니까 주로 집합을 대표하는 원소를 반환한다. 각 대표 원소들간의 파인드 결과를 비교하여 같은 집합 여부를 판단한다.
2. union
두 개의 집합을 하나의 집합으로 합친다.
3. make set
특정 한 원소만을 가지는 집합을 만든다.
++ 왜 트리를 사용하는가?
더 빠르기 때문
1. 배열에서
- 초기화: array[i] = i가 속한 집합의 번호(자기 자신)
- make_set(x): 원소 x에 대해 각각의 집합을 만든다.
- union(x,y): 모든 노드를 돌면서 y의 집합번호를 x의 집합번호로 변경
- 시간 복잡도는 O(N)
- find(x): x가 속한 집합 번호 찾기. 한번에 찾기 가능
- 시간복잡도 O(1)
- find는 빠르지만 union 연산이 느리다.
2. 트리에서
- 집합을 대표하는 번호 = 루트 노드 번호
- make_set(x): 원소 x에 대해 자기자신을 루트 노드로 생성
- union(x,y): x와 y의 루트노드를 찾은 후 y를 x의 자손으로 넣는다.
- 시간 복잡도는 O(N)보다 작음. find함수가 시간을 좌우
- find(x): x가 속한 루트노드 찾기, 재귀함수 사용
- 시간복잡도는 트리의 높이와 동일. 최악의 경우 O(N-1)
언제쓸까 대체...
1. kruskal 혹은 mst알고리즘에서 사이클 형성 여부 확인할 때
2. 집합연산을 하려할때... 집합의 포함관계 확인시 ex 백준 1717
UNION FIND의 기본 구현
/* 초기화 */
int root[MAX_SIZE];
for (int i = 0; i < MAX_SIZE; i++)
root[i] = i;
/* find(x): 재귀 이용 */
int find(int x) {
// 루트 노드는 부모 노드 번호로 자기 자신을 가진다.
if (root[x] == x) {
return x;
} else {
// 각 노드의 부모 노드를 찾아 올라간다.
return find(root[x]);
}
}
/* union(x, y) */
void union(int x, int y){
// 각 원소가 속한 트리의 루트 노드를 찾는다.
x = find(x);
y = find(y);
root[y] = x;
}
union-find 연산의 최적화하기
최악의 상황:

트리 구조가 완전 비대칭인 경우 = 연결 리스트 형태
트리의 높이가 최대가 된다.
원소의 개수가 N일 때, 트리의 높이가 N-1이므로 union과 find(x)의 시간 복잡도가 모두 O(N)이 된다.
배열로 구현하는 것보다 비효율적이다.
find 연산 최적화
경로 압축(path compression)사용 -> 시간복잡도 O(로그N)
요점: 트리를 타고 올라가면서 만나는 모든 부모노드를 루트노드에 직빵으로 연결해버린다. = 트리의 높이를 낮추기
/* 초기화 */
int root[MAX_SIZE];
for (int i = 0; i < MAX_SIZE; i++) {
root[i] = i;
}
/* find(x): 재귀 이용 */
int find(int x) {
if (root[x] == x) {
return x;
} else {
// "경로 압축(Path Compression)"
// find 하면서 만난 모든 값의 부모 노드를 root로 만든다.
return root[x] = find(root[x]);
}
}

union 연산의 최적화: union-by-rank(union-by-height)
요점 : rank에 트리의 높이를 저장한다.
항상 높이가 더 낮은 트리를 높은 트리 밑에 넣는다.
/* 초기화 */
int root[MAX_SIZE];
int rank[MAX_SIZE]; // 트리의 높이를 저장할 배열
for (int i = 0; i < MAX_SIZE; i++) {
root[i] = i;
rank[i] = 0; // 트리의 높이 초기화
}
/* find(x): 재귀 이용 */
int find(int x) { // 동일
}
/* union1(x, y): union-by-rank 최적화 */
void union(int x, int y){
x = find(x);
y = find(y);
// 두 값의 root가 같으면(이미 같은 트리) 합치지 않는다.
if(x == y)
return;
// "union-by-rank 최적화"
// 항상 높이가 더 낮은 트리를 높이가 높은 트리 밑에 넣는다. 즉, 높이가 더 높은 쪽을 root로 삼음
if(rank[x] < rank[y]) {
root[x] = y; // x의 root를 y로 변경
} else {
root[y] = x; // y의 root를 x로 변경
if(rank[x] == rank[y])
rank[x]++; // 만약 높이가 같다면 합친 후 (x의 높이 + 1)
}
}두원소가 속한 트리의 전체 노드 수 구하기
/* union2(x, y): 두 원소가 속한 트리의 전체 노드의 수 구하기 */
int nodeCount[MAX_SIZE];
for (int i = 0; i < MAX_SIZE; i++)
nodeCount[i] = 1;
int union2(int x, int y){
x = find(x);
y = find(y);
// 두 값의 root가 같지 않으면
if(x != y) {
root[y] = x; // y의 root를 x로 변경
nodeCount[x] += nodeCount[y]; // x의 node 수에 y의 node 수를 더한다.
nodeCount[y] = 1; // x에 붙은 y의 node 수는 1로 초기화
}
return nodeCount[x]; // 가장 root의 node 수 반환
}
참고: https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] Tree Traversal - Depth First Traversal (0) | 2020.10.04 |
|---|---|
| [알고리즘] Prefix Sum 구간 합/누적 합 알고리즘 (0) | 2020.10.01 |
| [알고리즘] Sliding Window 슬라이딩 윈도우 (0) | 2020.09.30 |
| [알고리즘] 그래프와 그래프 탐색 알고리즘 (0) | 2020.03.13 |
| [알고리즘] Floyd-Warshall 알고리즘 (0) | 2020.03.13 |

댓글