Implement pow(x, n), which calculates x raised to the power n (i.e. xn).
Example 1:
Input: x = 2.00000, n = 10 Output: 1024.00000
Example 2:
Input: x = 2.10000, n = 3 Output: 9.26100
Example 3:
Input: x = 2.00000, n = -2 Output: 0.25000 Explanation: 2-2 = 1/22 = 1/4 = 0.25
Constraints:
- -100.0 < x < 100.0
- -2^(31) <= n <= 2^(31)-1
- -104 <= xn <= 104
문제 풀이:
쉽네 하고 풀었는데 하나도 안쉬웠다.
n만큼 곱셈을 진행했더니 tle가 떴다. 왜냐면 n의 범위가 상당히 크기 때문..
두가지 방법으로 문제 해결이 가능하다.
1. 재귀함수 사용
기저 조건을 세워보자
if n=1 then return x
if n=0 then return 1
함수 식을 세워보자
if (n<0) then pow(1/x, -n);
if(n &1) n이 홀수면 return pow( x* x, n/2) *x;
else return pow(x *x, n/2);
n<0일때 주의사항이 있는데 음수의 범위는 -2^(31)까지이고 양수의 범위는 2^(31)-1이기 때문에 n이 int_min일 때 -1을 곱해버리면 overflow가 난다.
따라서 n이 int_min일 땐 먼저 x = x*x; n /=2;를 해줘야 한다.
식이 저렇게 나오는 배경은 2번 방법에서 알아보도록 하자.
class Solution {
public double myPow(double x, int n) {
if(n==0) return 1;
if(n==1) return x;
while(n == Integer.MIN_VALUE){
x = x*x;
n = n/2;
}
if(n<0) return myPow(1/x, -n);
double answer = myPow(x*x, n/2);
if(n%2 == 1) return answer * x;
return answer;
}
}
2. 모듈러 연산을 이용한 거듭제곱
모듈러 거듭제곱법이라는게 있는데 여기서 쓸 건 아니구 참고만..
빠른 모듈로 거듭제곱법 (개념 이해하기) | 암호학이란? | 칸아카데미
ko.khanacademy.org
1단계 아이디어만 이용하고자 한다.
거듭제곱을 할 때 2의 제곱수로 나타내면 O(로그2N)으로 계산가능하다.
5 ^ 37 제곱은 5 ^ ( 32 + 4 + 1)로 표현 가능하다.
즉 37 = 32 + 4 + 1 인데 다음과 같은 방법으로 37을 만들 수 있다.
37 -> 36 -> 18 -> 9 -> 8 -> 4 -> 2 - > 1 -> 0
X= 1에서 시작
IF N이 홀수 THEN 결과 * X
IF N이 짝수 THEN X = X*X; N = N>>1;
또 다른 예시 A^ 13제곱을 확인해보자
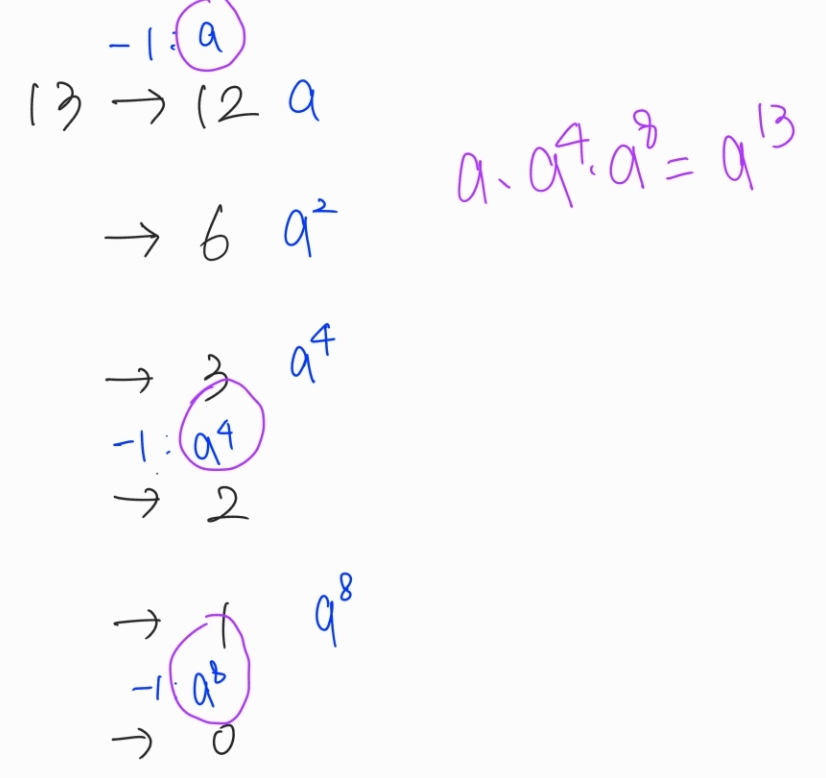
그래서 다음과 같은 코드가 나온다.
class Solution {
public:
double myPow(double x, int n) {
if(n==0 || x == 1){
return 1;
}
if(n==1){
return x;
}
int flag = 0;
if(n == INT_MIN){
x = x*x;
n = n>>1;
}
if(n<0){
flag = 1;
n = n * (-1);
}
long double result = 1;
while(n > 0){
if(n&1) {
result *= x;
}
x = x * x;
n = n>>1;
}
return (flag)? 1/result: result;
}
};
'알고리즘 문제풀이 > leetcode' 카테고리의 다른 글
| [leetcode 88] Merge Sorted Array (0) | 2020.11.19 |
|---|---|
| [leetcode 69] Sqrt(x) (0) | 2020.11.18 |
| [leetcode 26] Remove Duplicates from Sorted Array (0) | 2020.11.18 |
| [leetcode 189] Rotate Array (0) | 2020.11.16 |
| [leetcode 210] Course Schedule II (0) | 2020.11.16 |

댓글