Write a program to find the node at which the intersection of two singly linked lists begins.
For example, the following two linked lists:
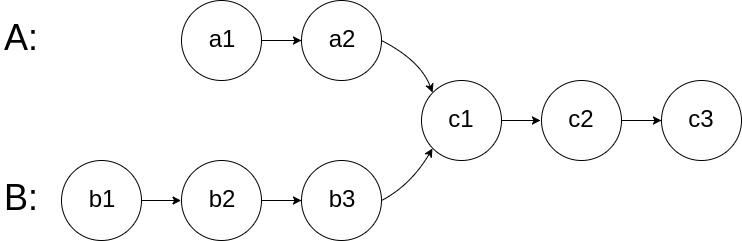
begin to intersect at node c1.
Example 1:
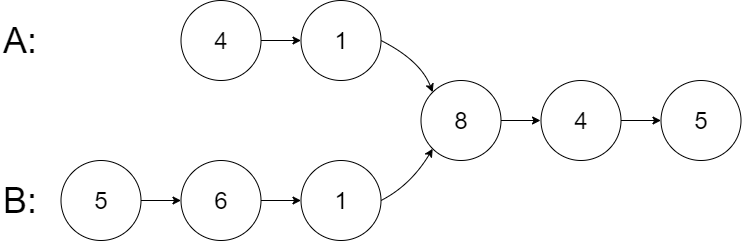
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 Output: Reference of the node with value = 8 Input Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
Example 2:
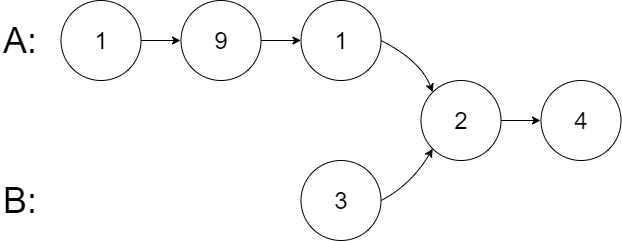
Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 Output: Reference of the node with value = 2 Input Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.
Example 3:
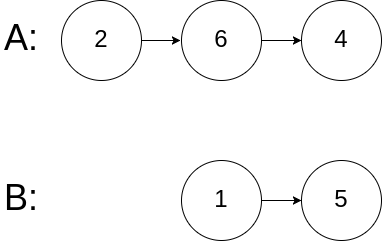
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 Output: null Input Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values. Explanation: The two lists do not intersect, so return null.
Notes:
- If the two linked lists have no intersection at all, return null.
- The linked lists must retain their original structure after the function returns.
- You may assume there are no cycles anywhere in the entire linked structure.
- Each value on each linked list is in the range [1, 10^9].
- Your code should preferably run in O(n) time and use only O(1) memory.
문제 풀이:
난이도는 분명 쉬움인데...쉽지 않다
maintain two pointers pA, pB initialized at the head of A and B.
Then let them both traverse through the lists, one node at a time.
1. When pA reaches the end of a list, then redirect it to the head of B.
pB가 리스트 마지막에 도착해도 마찬가지로 A의 헤드로 redirect햔다.
2. 만약 pA와 pB가 만난다면, pA 혹은 pB의 위차가 intersection node이다.
증명:
A = {1,3,5,7,9,11}
B = {2,4,9,11}
=> 9에서 만나야 한다. B가 짧으니까 pB가 리스트의 끝에 먼저 도달할 것이다.
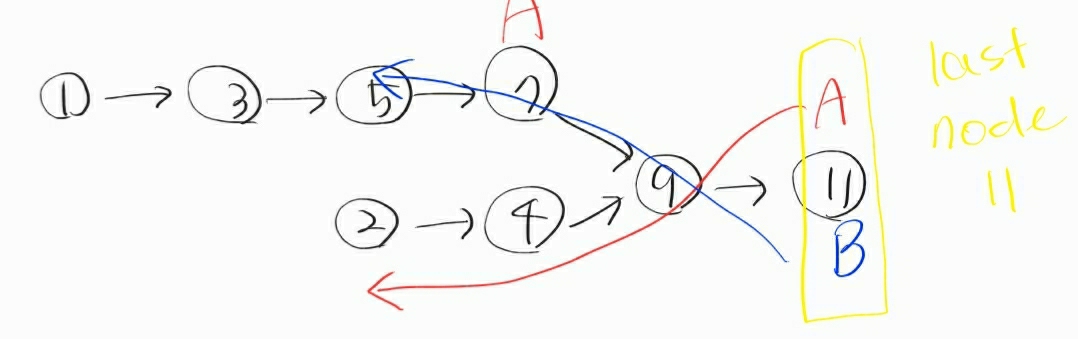
두 리스트가 교차한다면 무조건 하나의 노드에서 만난다.
즉 두 리스트가 교차한다면 두 리스트의 마지막 노드는 같아야 한다.
(교차 조건)
만약 교차한다면 두 리스트의 길이를 비교해야 한다.
리스트의 길이를 비교해서 출발지를 맞춘다. 위 예시에선 A가 2만큼 길기때문에 pA를 뒤로 두칸만큼 뒤로 밀어서 다시 두 리스트의 traverse를 시작한다.
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0;
int lenB = 0;
ListNode* cur = headA;
int lastA = 0;
while(cur != NULL){
lenA++;
lastA = cur->val;
cur = cur->next;
}
cur = headB;
int lastB = 0;
while(cur != NULL){
lenB++;
lastB = cur->val;
cur = cur -> next;
}
if(lastA != lastB){
return NULL;
}
ListNode* pA = headA;
ListNode* pB = headB;
if(lenA > lenB){
int diff = lenA - lenB;
for(int i=0; i<diff; i++){
pA = pA->next;
}
}else {
int diff = lenB - lenA;
for(int i=0; i<diff; i++){
pB = pB ->next;
}
}
while(pA != pB){
pA = pA->next;
pB = pB->next;
}
return pA;
}
};'알고리즘 문제풀이 > leetcode' 카테고리의 다른 글
| [leetcode 128] Longest Consecutive Sequence (0) | 2020.11.02 |
|---|---|
| [leetcode 148] Sort List (0) | 2020.11.02 |
| [leetcode 155] Min Stack (0) | 2020.11.01 |
| [leetcode 169] Majority Element (0) | 2020.11.01 |
| [leetcode 236] Lowest Common Ancestor of a Binary Tree (0) | 2020.10.31 |

댓글